DCT域自适应混沌加密的二值图像数字水印算法

目前，在保护数字作品的版权和安全问题上，有的学者结合密码学方面的知识，对带有版权信息的二值图像水印进行加密，然后嵌入到变换域的系数中，使受保护的数字产品具有双重安全性。而今天，我给大家介绍另外一种方法，利用人类视觉系统HVS对图像所具有的频率掩蔽、亮度掩蔽和对比度掩蔽等特性和混沌加密二值水印所具有的双重安全特性，一种基于DCT域中频的自适应混沌加密的数字水印算法应运而生。

基于DCT的混沌加密二值图像水印算法

本算法包括以下四个主要部分：对原始图像进行块分类、混沌产生随机序列、加密水印的产生和水印的嵌入和提取。

1、基于人类视觉系统（HVS）特性的块分类

人类视觉系统HVS对图像所具有的频率掩盖、亮度掩蔽和对比度掩蔽等效应表明：背景亮度越亮，纹理越复杂，人类视觉对其轻微变化就越不敏感，只要嵌入水印信号低于HVS的对比度门限（Contrast Sensitivity Threshold），HVS就无法感知到信号的存在，它具有如下三个特性：

①人眼对不同灰度具有不同的敏感性，通常对中等灰度最敏感，而且向低灰度和高灰度两个方向非线性下降；

②对图像平滑区的噪声敏感，而对纹理区的噪声不敏感；

③边缘信息对于人眼非常重要，必须保护边缘的质量不受大的损害。

因此，我们可以利用HVS特性选取不同的嵌入强度因子α以获得更好的视觉掩蔽性。

原始载体图像I（i，j）（1≤i≤N1，1≤j≤N2）为N1_N2个像素大小，每个像素为0~255灰度等级的灰度图像。首先将I分割成互不重叠的8×8的子块，(1≤i≤8，1≤j≤8，1≤n≤8），
B为原始载体图像所分的块数，且满足B=_(N1_N2/(8_8)_；然后对每一个子块In（i，j）进行DCT变换，得到In（u，v）；最后计算每个子块的灰度（或者亮度）的均值和方差，并以此作为块分类的依据：均值较小的块对应图像的平滑区域，均值较大的块对应的则可能是纹理区域或者边缘，其中纹理区域的方差较小而边界区域的方差较大。按上述方法可将所有图像块分为五类：第一类亮度较低，纹理简单，HVS对像素值的改变较为敏感，所嵌入的水印分量强度最小；第二类亮度中等，纹理中等，嵌入的水印分量强度较小；第三类亮度较高、纹理复杂，且不是边缘，HVS对像素值的改变敏感性较强，叠加的水印分量较小；其余为第五类。

2、混沌产生随机序列

混沌区的数据有两个特性：迭代不重复性和初值敏感性。当选定适当系数使方程进入混沌状态时，方程将进行无限不循环迭代，因此不会出现重复的迭代值。任何人如果不知道其初值（种子）0x都无法预测下一个迭代值，这种迭代的结果可以用来产生随机序列。一个一维离散的时间非线性动力系统可以定义为：

式中kx∈V，k=0，1，2，……。我们称状态τ：V→V是一个映射，它将当前状态kx映射到下一个状态1+kx。如果映射τ：V→V满足下面三个条件：

（1）具有对初始条件的敏感依赖性；

（2）是拓扑传递的；

（3）周期点在V中稠密。

则说对应的动力系统在V上是混沌的。

一类非常简单却被广泛研究的动力系统是Logistic映射，定义如下：

式中kx∈（－1，1），当μ＝4时，Logistic映射变成三角帐篷映射，我们采用的是三角帐篷映射：xk+1=4xk（1-xk），这个公式等价于：

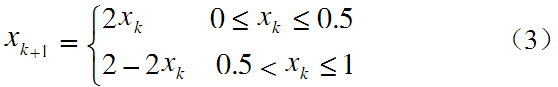
三角帐篷映射具有0均值，δlike自相关及互相关为0的特性。由该映射所产生的混沌序列具有以下优点：形式简单、对初始条件的敏感性、具有白噪声的统计特性。

根据公式产生的混沌序列是非周期且长度无限的实数序列，但在本文中只需要截取合适的长度，进而生成二值序列作为加密序列。由实值序列生成的二值序列的方法有很多种，如阈值门限法、多种量化方法等。本文采用阈值门限法，公式如下：

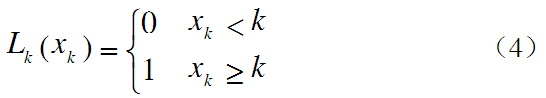
其中在本文中k取值为0.5，当xk<0.5时取0，否则取1。

3、加密水印的产生

水印W是大小为M1_M2(M1_M2=N1_N2/8*8)的二值图像，每个像素为0、1两种取值。二值图像水印W在嵌入原始载体图像之前，首先用混沌序列进行加密。加密过程如图所示：

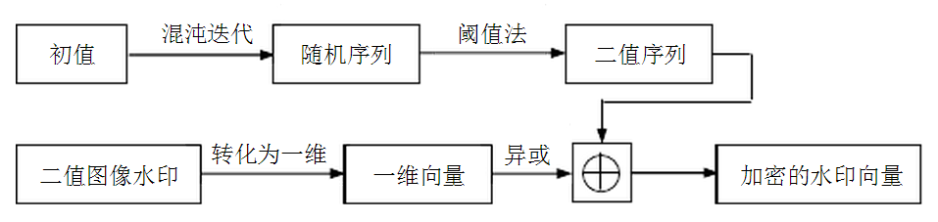
描述如下：将二维水印W转换为一维向量Wa的形式(a=1，2，_…，M1×M2)；然后，设定一个初值0x，按公式（3）进行迭代，得到混沌序列xk，然后进行阈值门限法得到0-1序列Lk
（k=1，2，…，M1×M2）；最后用生成的0-1序列Lk对二值水印图像进行加密，得到加密后的水印向量序列Wm=Wa⊕Lk=（m=1，2，_…，M1×M2），⊕在这里表示异或运算；混沌初值X0则可作为用户的私有密钥K。

经过以上处理的二值图像水印，同时具有初值敏感性和不可逆性，也即在不知道确切的初值的情况下，即使提取出水印信号也无法恢复出水印图像，从而提高了整个水印系统的安全性。

4、二值图像水印的嵌入和提取

（1） 水印的嵌入

水印嵌入过程由以下三个基本步骤组成，描述如下：

首先把原始载体图像I（i，j）（1≤i≤N1，1≤j≤N2）分成8×8大小不重叠的子块，对每个子块进行DCT变换，计算每个子块的方差和均值，对这些块进行分类，确定嵌入强度因子α。

其次是把二值水印图像W（u,v），(1≤u≤M1，1≤v≤M2，M1_M2=N1_N2/8*8)的系数矩阵变换成一个长为M1*M2的Wa向量，采用公式（3）产生一个混沌密码序列，截取合适的长度，并用阈值门限法将它转化为0-1序列Lk（1≤k≤M1_M2）；利用0-1序列kL对水印图像进行加密，得到加密序列Wm=Wa⊕Lk，⊕表示异或运算。

然后采用如下方法将加密序列Wm嵌入到原始图像的前两个DCT中频系数中。

其中，αn是不同种类块的嵌入强度因子。 最后对每块进行离散余弦反变换（IDCT），得到嵌有水印的图像I′。

（2）水印的提取

本文的水印提取是非盲文提取，需要原始图像，水印提取过程与水印嵌入的过程刚好相反，具体步骤如下：

首先对嵌有水印的图像I′进行DCT变换，计算每个块的亮度均值和方差，根据方差和均值对每一块进行分类，确定嵌入强度因子α。

其次提取出被加密的水印的向量W′m，利用初始值x0得到混沌加密序列，并用阈值门限法得到0-1序列Lk，得到解密的水印序列W′a=W′m⊕Lk。

最后将W′a转化为2-D的形式，得到提取出的水印图像W′。

本文提出了一种具有较强鲁棒性的数字水印算法，首先该算法通过对水印本身进行加密，这样水印攻击者即使获得水印数据，也不能提取正确的水印，从而为数字作品提供了双重保险；其次利用人类视觉系统(HVS)的特性自适应的把二值图像水印嵌入在DCT域的中频，既保障了水印的不可见性又保障图像的安全性。