基于二维可逆非线性映射的图像加密算法

根据一类二维可逆非线性映射具有单值确定的逆、本质非线性以及运算简单等适合构造加密算法的特点，提出适用于图像文件加密的新算法。这种加密算法将图像分成若干块，每块采用二维可逆非线性映射对各像素点的灰度值进行链式循环迭代，二维非线性映射的参数与迭代次数由一维混沌映射产生，克服了序列密码中存在的错误扩散问题，解决了由计算机精度引起的解密失败难题。

一、二维可逆非线性映射简介

二维非线性映射又被称为非平凡二维映像，它们必须为非线性的，至少是二次的。与一维映射不同，这类映射一般存在单值确定的逆．二维非线性映射中出现的折叠，可在不同的维上展开，而不压缩在一维上，非平凡二维映射所具备的这种性质与一维映射的特征有本质上不同。以Henon映射最为典型，Henon映像是最简单的非平凡二维映像，它是二次方型非线性的二维映射，它可以用于描述一般映射在指定轨道附近的动力学性质，这种映射已经足够复杂，分析其动力学性质时，通常很难作解析处理，数值方法不可避免，但是它们存在单值确定的逆。

Henon映射定义为：

其逆映射为：

Henon映射(1)、(2)切变换的雅可比矩阵(Jacobi)为：

Henon映射又被译之为伊依映射，b=1时为保面积映射，b<1时为耗散映射．它是Henon从研究球状星团以及洛伦兹吸引子中得到启发而于1 976年提出的。

二、二维可逆非线性映射在图像加密中的应用

下面以Henon映射为例讨论二维可逆非线性映射用于图像文件加密的原理与方法。

1、加密算法原理

将此类映射用于图像文件加密时，首先对图像分成若干块，分别进行块（组）处理。这是因为分块加密简单、快速，易于标准化，容易实现同步，同时，一个密文块（组）的传输错误不会影响到其他块，丢失一个密文块不会对随后的正确解密产生影响，克服了序列密码错误扩散的缺点。

在块内，采用由二维非线性映射（例如Henon映射）组成的处理单元对各像素点的灰度值进行链式循环迭代，由一维混沌映射产生的混沌序列改变二维非线性映射（例如Henon映射）的参数和迭代次数，基本加密、解密思路如图1所示：

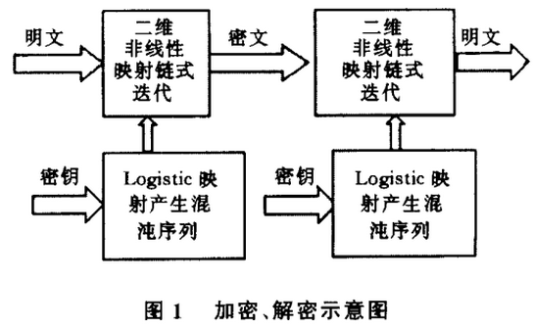
2、加密算法流程

加密算法应用二维取模的Henon映射，这里参数b=1，对各像素点的灰度值进行循环迭代，并用一维混沌映射产生的序列改变迭代次数d与Henon映射的参数a。

（1）加密算法步骤

记m×r图像I像素点的灰度值为A（x，y），令m×r=n，为便于描述加密算法记A（x，y）=A（rx+y），这样将二维位置下标表示的灰度值（x，y）记为一维位置下标表示的A（rx+y），即记为A1，A2，…，An。为简单起见，将以A1，A2，…，An为一个块来说明算法。实际应用时，可根据需要将图像明文分成若干固定大小的块（组）进行加密。

第一轮循环

第二轮循环

一般两轮循环已经足够，应用时可以进行多轮循环以获得更高的强度，最终的A1，A2，…，An-1，An是加密后的密文。

第一轮循环的示意图如图2所示。

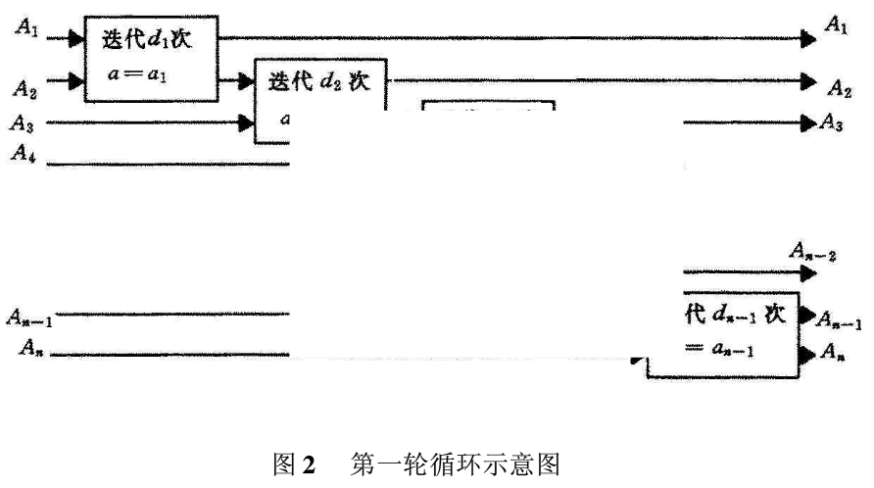
经过第一轮循环后，再进行第二轮循环：先将上面得出的新An，A1值用参数a=on的Henon映射迭代dn次得到的结果更新An，A1。再对刚得出的新的A1，A2，…，An-1，An重复第一轮循环。

（2）加密算法中迭代次数d与Henon映射

参数o取值的生成方法：迭代次数d1，d2，…，dn，d1'，d2'，…，d'n-1，……以及每次使用的Henon映射的参数a：a1，a2，…，an，a1'，a2'，…，a'n-1，都取值于由一维混沌映射生
成的混沌序列.

为简单起见，算法中将迭代次数d和Henon映射的参数口的取值都限制为[2，257]区间上的随机整数值.注意，这里限制了迭代次数不能为1，这是因为Henon映射含有一耦合项Yn+1=xn modG，如果迭代次数取为1，则有一项输入没有改变，这样会给密码攻击者留下信息。若需要增加复杂度，可以加大迭代次数，只要将区间[2，257]替换为更大的区间即可。

具体生成步骤如下：

a、用Logistic映射

产生一维混沌实数序列{Xn}，这里xn∈(0，1);

b、按如下规则将混沌实数序列xn映射为[2，257]区间上的整数序列{Xn}

若(k+ 1)/256≤Xn<(k+2)/256，则Xn=k，显然这样得到的Xn∈(2，3，…，257）。

给定初始值x0，参数μ0，迭代到ho次后记下用上述方法映射得到的整数混沌序列，依次赋值于d1，a1，d2，a2，...，dn，an，d'1，a'1，d'2，a'2，...，d'n，a'n。

（3）二维非线性Henon映射

为了适合图像文件加密的特点，在加密算法中使用的是如下变形的取模Henon映射，该映射存在单值确定的逆。

其逆映射为：

这里将Henon映射中的参数6设为1，如果6为其他数，在迭代过程中将会出现小数，这与像素点的灰度值都是长度为n个字节的整数不匹配，另外，由于图像像素点的灰度值有其上限，为防止运算溢出和数据量膨胀，这里对Henon映射变形进行了取模运算，其中G为像素点灰度值的最大值，例如灰度值长度为1个字节，则G= 256。

（4）加密算法实现

a、 输入参数

原始图像文件名Inlmage，结果图像文件名Outlmage，密钥（x0，μo，ho）。

a2'，...，d'n-1，a'n-1。

b、二维Henon映射对Lm×r，中各像素点的灰度值进行二轮循环迭代，得到一个密图

解密算法实现：用户只要正确输入密钥（xo，μ0，ho），将加密算法逆向运算即可获得解密图像。

3、 基于二维可逆非线性映射的图像加密算法分析

（1）Henon映射适合于构造链式循环迭代的加密算法

在采用非线性映射的加密算法中，必须要考察它们的逆运算，通常的非线性映射（如反三角函数）、混沌映射（如洛伦兹映射）等用于加密算法的一个难题就是它们的运算需要使用数值计算或变步长积分来解微分方程．这样由于计算机的有限精度效应与各计算机精度不同所产生的误差、及其在非线性运算中的误差传播与扩散与解密的正确性，实际运用受到很大限制。

Henon映射的这种可以求逆的信息处理功能特别适合于图像加密．因此采用此类二维非线性映射的加密算法，不仅可以保证加密解密的正确性，且速度远远快于DES分组加密，具有很高的实用价值。

（2） 密钥扩展算法的安全性

加密算法中由密钥控制非线性映射的参数与迭代次数的改变。迭代次数d1，d2，…，dn，d1'，d2'，…，d'n-1，……以及每次使用的Henon映射的参数a1，a2，…，an，a1'，a2'，…，a'n-1。实际上是密码学意义所需的足够安全长度的密钥，在加密算法中，它们由密钥种子又称为短密钥产生，通信双方共享一个短密钥（x0，μ0，h0），这里采用一维混沌映射的扩展算法将密钥种子扩展成所需的足够长的密钥，密钥扩展算法实际是一个伪随机序列发生器，该发生器的优劣直接影响分组密码的安全性，由于所产生的一维混沌整数序列X扎具有对初始条件值敏感、白噪声的统计特性等很好的密码学性质，又有容易生成，形式简单，便于软件实现等特点，所以采用混沌模型产生一维混沌整数序列的方法适合作为密钥扩展算法。

由于一维混沌整数序列具有的良好随机性，可以抵抗密钥相关攻击（即针对密钥扩展算法的弱点对分组密码进行的攻击），加密算法中密钥（x0，μo，ho）保持适当的长度，使穷举密钥攻击不易实施。

（3）算法的安全性分析

a、混淆性与扩散性

本加密算法中，由于二维非线性映射的循环迭代的作用，块（组）内每个像素点的灰度值完全扩散到其他的每一个像素点的灰度值中并变得面目全非，这符合香农信息论中的混乱与扩散两个设计准则。从加密算法可以看出，解密时从最后两项开始一步一步进行Henon映射的逆映射迭代，从后向前逐个将Im×r，中像素点的灰度值解出，且前面的解密正确与否影响到后面步骤地正确进行．如对16 x16图像，取迭代次数d1，a1，d2，a2，...，dn，an，d'1，a'1，d'2，a'2，...，d'n，a'n，为{2，3，…，257}中由混沌映射产生的数，穷举法的密钥空间为256256x4-2，对一般的图像取迭代次数为2或3就足够了。通过加密，明文随机混乱扩散到整个密文中，密文中未保留任何明文信息，包括明文的统计概率信息，并且彻底改变了图像的直方图的特征。

使用二维非线性映射的链式循环迭代所设计的密码使得明文、密文、密钥之间的依赖关系相当复杂，以至于这种依赖关系，即函数关系与统计关系对密码分析者来说无法利用。密钥的每一位数字影响密文的许多位数字，以防止对密钥进行逐段破译；明文的每一位数字也影响密文的许多位数字，以充分地隐蔽明文的统计特性，使得密码极具粘连性。

b、非线性度

非线性度分析的基本数学原理为：如果明文与密文的关系是n维线性关系，且系数是密钥，则n个明文密文对（而不是2n个）就可破解密钥；如果明文与密文的关系是n维r次函数关系，则n个明文密文对就可基本上破解密钥，这就是线性密码分析的原理．所谓非线性度即是抵抗线性密码分析的强度。在本加密算法中，由于使用了二维非线性映射循环迭代的方法，由密钥控制非线性映射的参数与迭代次数的改变，链式中每迭代d次就加入新的数据，若块内有n个像素点灰度值作为明文，则明文与密文的关系大致是n维、r=2（d1，d2，…，dn，d1'，d2'，…，d'n-1...）次，欲破解此密钥就需要nr个明文密文对，由于r非常大，所以足以保证其安全性．另外，由于每迭代d次就加入下一个像素点的灰度值，这就使得要找到一个非常逼近明文与密文的n维线性关系几乎不可能，试验表明神经网络的逼近方法对这种变参数的非线性模型也无能为力。

c、安全强度的稳定性

近年来混沌保密系统受到质疑，Dedieu等用参数自适应同步控制的方法对混沌系统的参数（密钥）进行辨识，从而达到破解的目的，所以许多简单的低维混沌映射加密算法保密性能不够安全，察其原因主要是由混沌方程产生的类随机流不是数学意义上的理想状态，同一混沌方程连续多次迭代，例如超过几百万次，由于计算机精度造成的舍入误差，混沌的类随机流将变成巨型周期，这为密钥带来一定信息，本加密算法中，只用混沌映射作为密钥扩展算法，使得混沌序列的长度大大缩短，其长度远小于由舍入误差导致的巨大周期，所以可以看成是随机序列，大大减小了密钥、明文密文对相互之间的相关性，同时，由于采用的混沌序列长度很短，这就使得密码攻击者无法取得足够多的样本数据，进而辨识出混沌系统的参数（密钥）．另外，在本加密算法中，由于密钥的各位对安全性的贡献是相对平均的，即密钥之间的相关性很弱，即使部分密钥被破译后，也很难得出其他密钥的信息，以上这些措施充分保证了密码安全强度的稳定性。

三、实验结果比较

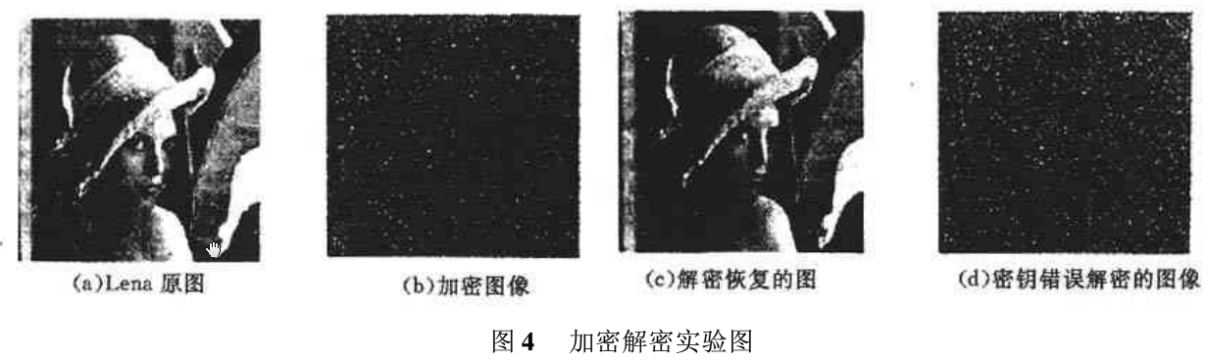
采用本文方法对多幅图像进行试验，图4为该加密算法对Lena图像文件加密与解密结果，图4(b)的密钥为x0 =0．65834，μ0=3.7853，ho=200。图4(d)错误密钥为x0=0.65833，μ0=3.7853，ho=200。

由实验结果可以看出，加密后的图像呈地毯状均匀分布，密钥正确时，解出的图像无误，当密钥错误时，解密得出的图像与原图像相比较面目全非，得不到有用的信息，直方图也呈现均匀分布，这里不再列出。

基于动态信任的内生安全架构

动态信任是一种新型的信息安全架构，近年来随着物联网、云计算和移动化等技术的发展而逐渐受到关注。传统的信息安全架构往往是建立在固定的信任模型之上，而动态信任则更加灵活和自适应，可以根据实际情况动态调整信任度，从而提高整个系统的安全性。本文将从以下几个方面来探讨基于动态信任的内生安全架构，包括动态信任的概念、功能特点、应用场景、实现方法等。

一、动态信任的概念

动态信任是指基于多方交互和数据分析，根据实时风险评估结果自适应调整信任度的一种信任模型。它与传统的访问控制模型不同，传统模型是基于身份验证和访问授权来限制访问权限的，而动态信任则更加注重实时风险评估和动态调整信任度。动态信任由于其灵活性和自适应性被广泛应用于物联网、云计算和移动化等领域，成为一种新型的内生安全框架。

二、动态信任的功能特点

1、实时风险评估
动态信任的核心是实时风险评估，通过对多方交互数据的分析、模型预测和机器学习等方法，从而实现对用户、设备、应用以及网络等方面的风险评估。同时，动态信任支持多种评估方法，可以根据实际情况选择不同的评估方法来评估系统的安全性。

2、动态调整信任度
动态信任可以根据实时风险评估结果自适应调整信任度，从而提高整个系统的安全性。例如，对于一个新的设备或应用，由于缺少足够的信任度，系统可以限制其访问权限，等到其表现良好后再逐步增加信任度。另外，在不同的应用场景中，可以根据不同的容错需求设置不同的信任阈值，从而更加灵活地调整系统的安全性。

3、安全事件的自适应响应
基于动态信任的内生安全框架可以根据实时风险评估结果自适应响应安全事件，例如实时阻断异常访问或异常信任行为等，从而保护整个系统的安全。另外，动态信任还可以实现安全威胁预警和安全日志审计等功能，为后续的安全事件响应提供支持。

三、动态信任的应用场景

基于动态信任的内生安全框架适用于物联网、云计算和移动化等领域，可以提高系统的安全性和稳定性。具体应用场景如下：

1、物联网领域
对于物联网场景，动态信任可以实现对设备、应用、用户等的实时风险评估和动态信任管理，从而保护整个物联网系统的安全。例如，可以基于设备的行为、属性等数据进行风险评估，判断设备是否存在安全风险，并进行相应的防御措施。

2、云计算领域
对于云计算场景，动态信任可以实现对用户、应用、网络等的实时风险评估和自适应调整信任度，从而提高整个云计算系统的安全性和稳定性。例如，可以根据用户的访问情况和应用的行为数据等进行风险评估，判断用户和应用是否存在安全风险，并相应的限制其访问权限。

3、移动化场景
对于移动应用场景，动态信任可以实现对应用、用户等的实时风险评估和自适应调整信任度，从而保护整个移动应用系统的安全。例如，可以根据应用的行为数据、用户的位置信息等进行风险评估，判断应用和用户是否存在安全风险，并相应的限制其访问权限。

四、动态信任的实现方法

基于动态信任的内生安全框架的实现方法主要包括以下几个方面：

1、机器学习技术
机器学习技术可以实现对多方交互数据的分析和预测，进而实现实时风险评估和动态信任管理。例如，可以使用支持向量机、神经网络、朴素贝叶斯等算法对数据进行分类和预测，从而实现安全风险评估。

2、分布式计算技术
分布式计算技术可以实现对大规模数据的分析和处理，多种评估方法的实现和系统的扩展性等。例如，可以使用MapReduce等分布式计算技术来实现大规模数据的分析和处理，从而提高系统的效率和准确性。

3、安全日志管理技术
安全日志管理技术可以实现对安全事件的记录、分析和响应等功能，从而提高系统的安全性和稳定性。例如，可以使用SIEM技术来实现安全事件的实时监测、分析和响应，从而提供相应的安全保障。

总之，基于动态信任的内生安全框架是一种新型的信息安全架构，其具有灵活性和自适应性等特点，可以根据实际情况动态调整信任度，提高整个系统的安全性。在物联网、云计算和移动化等领域具有广泛的应用前景，同时也面临着各种技术挑战和安全威胁。因此，我们需要进一步探索动态信任技术的研究和应用，并积极探索基于动态信任的内生安全框架的实现方法和应用策略，从而实现网络信息安全的可靠保障。

本文为收集整理，文章部分观点不代表本站观点，如有侵权或其它问题请反馈客服。https://www.wgj7.com/cjwt/16337.html